1. Introduction▲
La cryptographie, c'est la science du chiffrement et du déchiffrement d'informations, dans le but de les rendre illisibles par des non-initiés. Cependant, le chiffrement est toujours déchiffrable et la durée de vie de la confidentialité dépendra de l'investissement sur la force du chiffrement.
En informatique, c'est la base de tout échange sécurisé. La notion de sécurité inclut non seulement l'aspect confidentiel, mais également l'authentification des partenaires.
C'est une science très hautement mathématique et nous n'aborderons pas du tout cet aspect ici, c'est vraiment une affaire de spécialistes, et je n'en suis pas un.
Nous verrons plutôt comment mettre en œuvre de tels procédés et dans quel cadre les utiliser, car la cryptographie n'est finalement qu'une fonctionnalité. Elle peut être appliquée à peu près à tous les niveaux du modèle OSI, principalement au niveau IP (avec par exemple IPsec) et au niveau des applications. À peu près tous les protocoles de haut niveau (HTTP, FTP, POP, IMAP…) peuvent la mettre en œuvre. Il y a également SSH, le shell distant sécurisé, qui permet, entre autres, de disposer d'un terminal distant, un peu comme Telnet, mais avec plus de sécurité.
Une application des plus intéressantes dans le domaine des réseaux est certainement la réalisation d'un tunnel sécurisé. Un tel procédé permet l'établissement d'un « réseau privé virtuel » (VPN) à travers un réseau de faible sécurité, comme l'internet, en créant une liaison point à point entre deux hôtes. La cryptographie intervient pour sécuriser cette liaison, pour la rendre « étanche ».
Nous allons mettre en place un tel tunnel avec le chapitre Open VPN, et ce tunnel, nous allons le sécuriser au moyen d'OpenSSL.
2. Position du problème▲
2-1. Rendre un message incomprĂ©hensible par le non-initiĂ©▲
Transmettre de l'information de telle manière que seuls les initiés puissent l'utiliser n'est pas un concept nouveau, il est même la base de la communication.
Un internaute qui ne connaît pas le français sera bien incapable de comprendre quoi que ce soit à la lecture de ces pages. Dans l'exemple, cependant, rien n'interdit à cet internaute d'apprendre le français pour en déchiffrer le contenu. Tout le monde peut apprendre le français, il n'y a aucun secret dans cette langue (juste pas mal de difficultés, mais pas de secret).
Dans de nombreux cas, cette « protection » ne sera donc pas satisfaisante.
Pour qu'un langage devienne un moyen de transfert de données confidentielles, il faut que l'apprentissage de ce langage soit impossible. Impossible n'étant pas français, il faudra donc se contenter d'en rendre l'apprentissage le plus difficile possible.
2-1-1. Juste un algorithme secret▲
Il peut s'avérer nécessaire de créer un langage spécifique, confidentiel, dont l'apprentissage reste difficile, idéalement impossible, pour le non-initié. Dans un tel cas, nous disposons d'un algorithme de chiffrement qui assure à lui seul la confidentialité du message. Aussi longtemps que cet algorithme ne sera partagé que par les seules personnes autorisées, le secret restera inviolé.
Un tel procédé, cependant, n'est pas considéré comme sûr. Que quelqu'un réussisse à reconstituer l'algorithme et il n'y aura plus de secret.
La réussite du procédé repose sur le fait qu'un nombre minimal de personnes sont dans le secret. Il se trouve que pour qu'un système soit réellement efficace, il faut qu'un maximum de personnes puissent en étudier le mécanisme, pour découvrir toutes les failles qu'il peut contenir. Il y a donc ici une incohérence fondamentale.
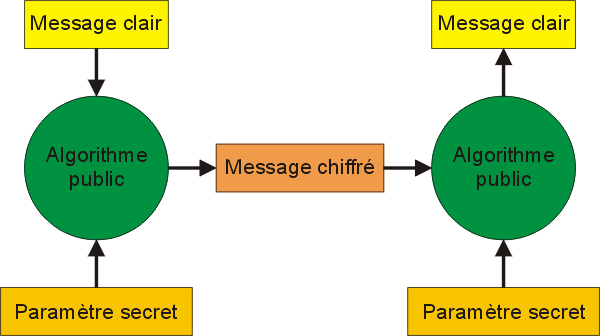
2-1-2. Un algorithme et une clĂ©▲
Il est largement préférable d'utiliser un algorithme public, que tout le monde peut analyser et utiliser, mais qui exploitera un paramètre de chiffrement qui, lui, ne sera pas partagé. Si l'on ne connaît pas la valeur de ce paramètre, même en disposant de l'algorithme, il sera impossible de déchiffrer le message. Le paramètre secret s'appelle une clé de chiffrement.
Ce principe, qui peut éventuellement adopter des combinaisons de clés, comme nous le verrons plus loin, reste à l'heure actuelle le procédé le plus sûr. Ici, pour déchiffrer le message, il « suffira » de trouver la bonne clé, l'algorithme étant public. La difficulté avec laquelle une clé non connue pourra être retrouvée sera seule garante du secret.
En ce qui concerne l'algorithme, comme chacun peut l'utiliser et l'analyser, s'il possède une faille, elle sera facilement et rapidement découverte et corrigée.
2-2. Cacher un message dans un autre message▲
Il peut être amusant, utile, nécessaire, voire les trois à la fois, de cacher un message dans un autre. Un message chiffré, on voit qu'il est chiffré et on essaye de le déchiffrer. Un message caché, on ne le voit pas et donc on ne cherche pas à le retrouver si l'on ne sait pas qu'il existe.
La science de la dissimulation d'un message dans un autre s'appelle la stéganographie.
Bien que cette approche n'entre pas dans le cadre de cet exposé, il est intéressant de savoir que ça existe.
Un exemple classique s'il en est (sous réserve d'authenticité) : une correspondance écrite entre George Sand à Alfred de Musset.
George écrit ceci à Alfred :
| Je suis très émue de vous dire que j'ai bien compris, l'autre jour, que vous avez toujours une envie folle de me faire danser. Je garde un souvenir de votre baiser et je voudrais que ce soit là une preuve que je puisse être aimée par vous. Je suis prête à vous montrer mon Affection toute désintéressée et sans cal- cul. Si vous voulez me voir ainsi dévoiler, sans aucun artifice mon âme toute nue, daignez donc me faire une visite Et nous causerons en amis et en chemin. Je vous prouverai que je suis la femme sincère capable de vous offrir l'affection la plus profonde et la plus étroite Amitié, en un mot, la meilleure amie que vous puissiez rêver. Puisque votre âme est libre, alors que l'abandon où je vis est bien long, bien dur et bien souvent pénible, ami très cher, j'ai le cœur gros, accourez vite et venez me le fait oublier. À l'amour, je veux me sou- mettre. |
Comme c'est beau, comme c'est joliment dit, comme c'est poétique (normal, c'est George Sand, quand même) !
Bon, maintenant, lisez le texte, mais seulement une ligne sur deux, en sautant les lignes paires. Vous constaterez que le message devient tout de suite nettement plus direct…
Et, pour continuer la démonstration, lisez donc la réponse que fait Alfred de Musset :
| Quand je vous jure, hélas, un éternel hommage Voulez-vous qu'un instant je change de langage Que ne puis-je, avec vous, goûter le vrai bonheur Je vous aime, ô ma belle, et ma plume en délire Couche sur le papier ce que je n'ose dire Avec soin, de mes vers, lisez le premier mot Vous saurez quel remède apporter à mes maux. |
Lisez bien, l'astuce stéganographique est fournie avec.
Georges Sand, qui n'est pas de celles qui abandonnent en chemin, conclut de la sorte :
| Cette grande faveur que votre ardeur réclame Nuit peut-être à l'honneur mais répond à ma flamme. |
À quoi bon perdre son temps en attentes inutiles. Plus vite c'est fait, plus vite on pourra le refaire…
Il est possible d'inventer une foule de façons de dissimuler un message dans un autre
Avec l'information numérique, il devient possible de cacher à peu près n'importe quoi dans n'importe quoi. Souvent dans des images.
Il est aussi possible, au cas où, d'utiliser une méthode de chiffrement sur le message caché.
2-3. Un peu de vocabulaire▲
Ce qui suit est directement inspiré de l'ouvrage :
Cryptographie Appliquée
De Bruce Schneier
Traduit en français par Laurent Viennot
Publié chez Vuibert.
Une sorte de bible pour qui veut approfondir sérieusement le sujet.
- Un message en texte clair est un message que tout le monde peut interpréter, soit directement, soit avec un outil de traduction (un dictionnaire et une grammaire par exemple).
- La transformation d'un message pour le rendre incompréhensible, même avec un outil de traduction est appelée chiffrement (encryption, éventuellement).
- Le résultat du chiffrement donne un texte chiffré (ou cryptogramme).
- L'action inverse s'appelle le déchiffrement, elle permet de restituer le texte en clair.
- L'art de chiffrer et de déchiffrer s'appelle la cryptographie, les spécialistes en la matière sont des cryptographes.
- Ceux qui s'amusent à essayer (et parfois même à arriver) à déchiffrer un message sans en connaître la ou les clés sont les cryptanalystes, ils font de la cryptanalyse.
- La branche mathématique sur laquelle s'appuient la cryptographie et la cryptanalyse s'appelle la cryptologie et les spécialistes de cette chose sont les cryptologues.
2-4. Un peu de philosophie▲
Comme il est illusoire de penser que l'on pourra mettre un jour au point un procédé de chiffrement qui ne sera jamais « cassable » par un cryptanalyste, il faut se résoudre à considérer qu'un système de chiffrement est forcément vulnérable et donc l'utiliser dans un domaine où il conservera son maximum d'efficacité.
Ce domaine d'efficacité peut s'évaluer en considérant quelques critères :
- les efforts déployés pour casser un chiffrement seront proportionnels à l'intérêt qu'il y a à obtenir les données déchiffrées (obtenir le moyen de déchiffrer des transactions bancaires peut être plus motivant que de percer le secret d'un e-mail que M. X envoie à Mlle Y) ;
- pour casser un chiffrement, il faut de la puissance de calcul (puissance=effort/temps). Il faut donc utiliser un chiffrement pas plus longtemps que le temps nécessaire à le casser, avec les moyens de calculs supposés pouvoir être mis en œuvre par les attaquants (les moyens incluent non seulement le potentiel de calcul, mais également les algorithmes de recherche) ;
- plus le volume de données chiffrées avec la même méthode est important, plus il fournit aux attaquants du matériel de travail, il faut donc ne pas dépasser un volume critique avec le même chiffrement ;
- une information n'a généralement pas besoin de rester indéfiniment secrète. « Demain, on débarque sur les plages de l'Atlantique ». Après-demain, cette information n'aura plus besoin de rester secrète. Il suffit donc de trouver un procédé de chiffrement qui puisse résister 24 h.
Il faut comprendre de tout ceci que la sécurité introduite par un procédé de chiffrement reste relative. Elle n'est fonction que de l'efficacité du procédé en rapport à l'intérêt qu'il y a à le casser.
3. Les clĂ©s du chiffrement▲
RĂ©sumons-nous.
En cryptographie numérique, chiffrer une information consiste à modifier la suite d'octets qui constituent cette information au moyen d'un algorithme mathématique.
L'algorithme étant normalisé, il peut être connu de tout le monde. Ainsi, pour que le secret soit assuré, il faudra que cet algorithme utilise un paramètre supplémentaire appelé une clé. Une information chiffrée avec un algorithme connu restera déchiffrable par les seuls possesseurs de la clé appropriée, même si l'algorithme est connu de tous. Les clés de chiffrement sont donc les éléments essentiels dans la garantie du secret souhaité.
Une fois le procédé mis en place, nous pouvons en attendre quelques services.
3-1. ConfidentialitĂ©▲
L'usage auquel on pense en premier est naturellement la confidentialité des données. Le premier désir est bien que les messages ne soient lisibles que par les seules personnes autorisées.
C'est bien, mais c'est loin de suffire, pour assurer une totale relation de confiance.
3-2. ContrĂ´le d'intĂ©gritĂ© et authentification▲
3-2-1. IntĂ©gritĂ©▲
Dans certains cas, il peut être nécessaire d'assurer simplement que les données sont intègres, c'est-à -dire qu'elles n'ont pas été au passage falsifiées par un intrus. Ces données restent « claires », au sens où elles ne sont pas secrètes.
Un exemple simple : je propose en téléchargement un fichier contenant une application informatique. Je voudrais éviter qu'un intrus ne puisse, par un moyen quelconque, dénaturer mon application et y introduisant, par exemple, un « root kit ».
Mon code est sous licence GPL, les sources sont disponibles, je ne veux pas rendre mon application secrète, je veux juste en assurer l'intégrité du code.
Je vais donc réaliser un « résumé concis » de mon fichier, typiquement une somme MD5(1) ou SHA(2).
Ce résumé est suffisamment précis pour qu'il puisse mettre en évidence toute modification ultérieure de mon fichier. Bien sûr, nous parlons ici de mathématiques. Un résumé MD5 d'un fichier contenant l'image ISO d'un DVD ROM d'installation d'une distribution Linux, par exemple, serait de la forme : 5025c41edf87b679f036377013234d9b (MD5sum du DVD d'installation de la fedora core 2).
Ce résumé concis, ou empreinte, dispose de caractéristiques fondamentales :
- l'empreinte d'un message est complètement significative de ce message. Il n'y a pratiquement aucune chance que deux messages différents puissent avoir la même empreinte ;
- la modification d'un seul bit dans le fichier original va considérablement modifier son empreinte ;
- le procédé est irréversible, c'est-à -dire qu'il est extrêmement difficile de reconstituer le message à partir de son empreinte.
Bien. Mais sans précautions supplémentaires, ça ne va pas suffire, parce que celui qui arrivera à corrompre mon fichier en téléchargement pourra sans doute modifier aussi l'empreinte, pour qu'elle soit celle du fichier corrompu.
Une empreinte, si elle utilise bien un procédé de chiffrement, ne dispose pas d'un secret. L'algorithme utilisé (MD5, SHA…) est public et s'il n'est pas possible de reconstituer un message à partir de son empreinte, il est en revanche tout à fait possible pour quiconque de recalculer une empreinte après modification de l'information.
Typiquement, une somme MD5, sans précautions particulières, ne servira qu'à vérifier que le fichier n'a pas été corrompu lors du téléchargement, mais elle n'apportera pas la preuve de l'authenticité du fichier en téléchargement.
Il faudra donc trouver en plus, un moyen pour certifier l'authenticité de cette empreinte.
3-2-2. Authentification▲
Il s'agit d'apporter par la cryptographie la preuve que le message est bien authentique. Compte tenu de ce que nous venons de voir, il suffira dans la plupart des cas de pouvoir assurer que l'auteur de l'empreinte du message est bien celui qu'il prétend être. Il s'agit en quelque sorte d'une lettre manuscrite, non raturée et signée.
3-2-3. Non-rĂ©pudiation▲
C'est le corollaire direct de l'authentification. Celui qui a rédigé une lettre manuscrite, non raturée et signée de sa main, ne pourra en aucun cas prétendre par la suite qu'il n'en est pas l'auteur. Il en va de même pour l'authentification numérique.
3-3. Les clĂ©s, leurs types et leurs utilitĂ©s▲
Il y a deux types de clés :
- les clés symétriques, on chiffre et déchiffre avec la même clé ;
- les clés asymétriques, avec une clé publique et une clé privée, ce qui est chiffré avec l'une ne peut être déchiffré qu'avec l'autre.
Les deux clés sont uniques et sont liées l'une à l'autre, mais si la clé privée reste confidentielle, la clé publique, elle, peut être copiée à volonté.
Il s'agit en fait d'un abus de langage. Les clés ne sont pas symétriques ni asymétriques, ce sont les procédés de chiffrement qui le sont.
3-4. Chiffrement symĂ©trique▲
C'est le plus facile à comprendre, c'est aussi la méthode de chiffrement la plus facile à réaliser et qui consomme le moins de ressources de calcul et de bande passante.
Les deux hôtes qui doivent échanger des données confidentielles (secrètes) disposent tous les deux d'une clé identique. L'émetteur chiffre les données avec, puis les envoie au récepteur. Ce dernier déchiffre avec la même clé pour récupérer des données lisibles.
Cette méthode assure la confidentialité des données, celui qui intercepterait la communication ne pourra pas lire les données échangées tant qu'il n'aura pas pu se procurer la clé. Il n'y a aucune authentification de faite sur l'émetteur comme sur le récepteur, sauf si deux personnes seulement disposent de la clé.
Le principal souci avec cette méthode, c'est qu'il faut s'échanger la clé et lors de cet échange, sans précautions particulières, n'importe quoi peut se produire.
3-5. Chiffrement asymĂ©trique▲
Cette méthode permet de faire aussi bien l'authentification que la confidentialité des données. Il est évidemment possible de combiner les deux.
3-5-1. Principes de base▲
Là , c'est un peu plus complexe et il vaut mieux bien suivre pour ne pas se perdre :
- chaque personne dispose d'un jeu de clés comportant :
- une clé privée : elle est unique et confidentielle, elle appartient exclusivement à l'hôte concerné, il ne la distribue à personne, aucun double de cette clé ne doit être créé,
- une clé publique : elle est unique également, mais tout le monde peut s'en procurer une copie, il suffit d'aller la chercher chez un dépositaire, dit « tiers de confiance ». Il s'agit en quelque sorte d'un concierge qui garde ces clés publiques et certifie qu'elles appartiennent bien à la personne indiquée ;
- ce qui est chiffré avec une clé publique ne peut être déchiffré qu'avec la clé privée correspondante ;
- ce qui est chiffré avec la clé privée ne peut être déchiffré qu'avec la clé publique correspondante.
Tout ceci peut à première vue paraître absurde, puisqu'il y a à chaque fois une clé qui peut être récupérée par n'importe qui. Oui mais…
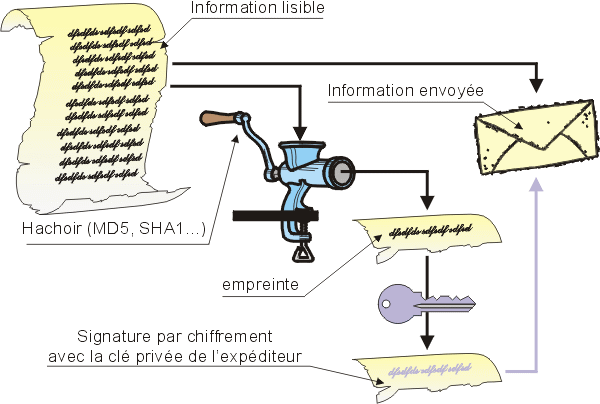
3-5-2. Authentification▲
Je réalise une empreinte avec un algorithme non réversible (MD5, SHA…). Cette empreinte ne permet pas de reconstruire le message original, mais elle représente « à coup sûr » un résumé de mon message original. Un simple bit modifié dans le message donnerait une empreinte complètement différente.
Je chiffre cette empreinte avec ma clé privée et l'envoie, avec le message en clair, au destinataire.
Mon message n'est pas confidentiel, il est envoyé en clair. Mais :
- l'empreinte réalisée est intimement attachée au contenu de mon message, si le message est intercepté et modifié, l'empreinte devra être recalculée,
- comme l'empreinte a été signée avec ma clé privée, je suis le seul à pouvoir le faire, donc toute modification ultérieure à l'envoi ne pourra pas être signée avec la bonne clé (aussi longtemps que ma clé privée restera secrète).
Lorsque le destinataire recevra le message signé :
- le destinataire recalcule l'empreinte du message reçu ;
- il déchiffre l'empreinte signée avec la clé publique de l'expéditeur ;
- il compare les deux empreintes. Si elles sont identiques, c'est que le message :
- est bien conforme Ă l'envoi, puisque les empreintes sont identiques,
- est bien envoyé par l'expéditeur propriétaire de la clé publique avec laquelle l'empreinte signée a été déchiffrée.
Voilà résolu le problème de la signature (authentifiée). Ce type de signature engage l'expéditeur. Il ne peut nier avoir envoyé cette information, puisqu'il l'a signée sans falsification possible, pour autant que l'on soit sûr de l'authenticité de la clé publique.
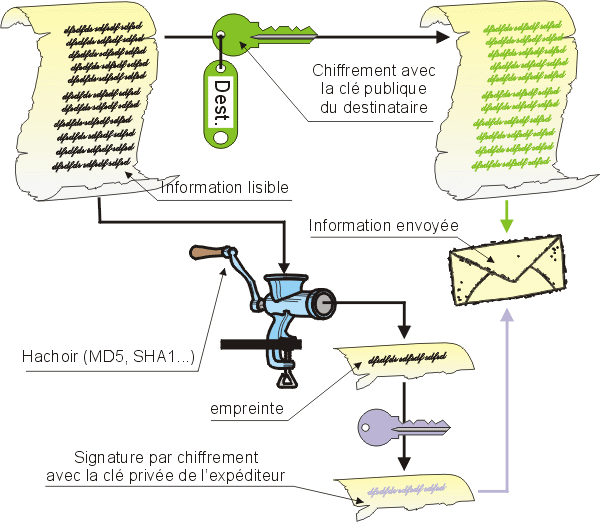
3-5-3. ConfidentialitĂ©▲
Je chiffre mon information avec la clé publique du destinataire, et je lui envoie cette information. N'importe qui peut faire de même, puisque le chiffrement se fait avec une clé publique. N'importe qui peut récupérer la clé publique de n'importe qui chez le concierge.
Donc, le message n'est pas authentifié, mais :
- comme j'ai chiffré avec la clé publique du destinataire, le message sera illisible pour qui ne détiendra pas la clé privée correspondante ;
- comme seul le bon destinataire, normalement, détient cette clé privée, il sera le seul à pouvoir déchiffrer le message.
Je n'ai pas pu m'authentifier auprès du destinataire, mais j'ai pu lui envoyer un message confidentiel, puisqu'il est le seul à pouvoir le déchiffrer.
3-5-4. Les deux▲
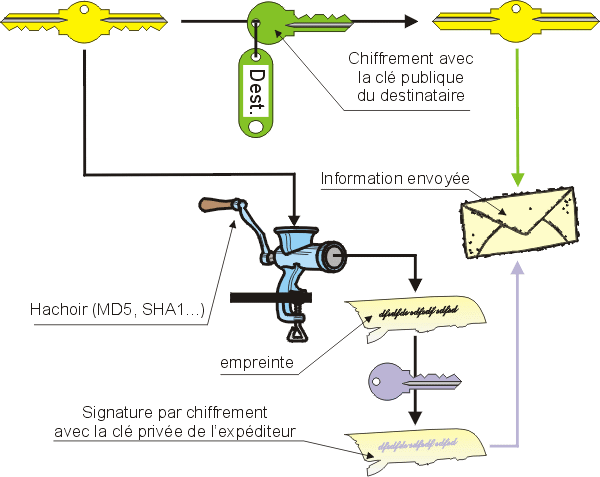
Vous avez compris le principe ? Alors, faire les deux devient simple :
- je réalise une empreinte de mon message et je la chiffre avec ma clé privée pour l'authentifier ;
- je chiffre le message lui-même avec la clé publique du destinataire pour le rendre confidentiel ;
- j'envoie le tout au destinataire.
Le destinataire déchiffrera le message avec sa clé privée, en calculera localement l'empreinte, puis déchiffrera l'empreinte envoyée avec ma clé publique :
- comme il est le seul à pouvoir déchiffrer avec sa clé privée, le message est bien confidentiel ;
- comme je suis le seul à pouvoir chiffrer l'empreinte avec ma clé privée, le message est bien authentique.
Bon. Ça roule, mais vous comprenez bien que l'opération est lourde :
- il faut chiffrer et déchiffrer deux fois au lieu d'une, comme on le ferait avec une clé symétrique ;
- le chiffrement/déchiffrement avec des clés différentes est une opération mathématique plus lourde, plus coûteuse en ressources CPU.
Rappelons que le principal problème du chiffrement symétrique est qu'il faut s'échanger l'unique clé à un moment donné et que, lors de cet échange, quelqu'un pourrait l'intercepter.
Ce problème va être résolu magistralement de la façon suivante.
3-6. Un Ă©change authentifiĂ© et confidentiel▲
Dans un échange d'informations (tunnel VPN par exemple), l'idéal, pour économiser les ressources CPU et augmenter le débit de l'échange, serait de trouver un moyen sûr d'échanger entre les partenaires une clé symétrique. Avec ce que nous savons, c'est relativement facile à réaliser.
Dans un premier temps, je fabrique une clé symétrique, à usage limité dans le temps, que nous appellerons une clé de session.
Je vais envoyer à mon interlocuteur cette « clé symétrique », que je vais authentifier et rendre confidentielle par les méthodes vues plus haut.
Et voilà le travail. Nous sommes deux à disposer de la même clé, transmise par une voie sécurisée.
La suite de l'échange pourra être chiffrée et déchiffrée avec cette clé de façon symétrique. Mais comme ça ne suffit pas, cette clé aura une durée de vie assez courte, quitte à devoir en échanger une nouvelle en cours de dialogue.
En effet, un intrus qui suivrait la discussion pourrait, au moyen d'outils faits exprès pour, finir par découvrir la clé symétrique, parce qu'il dispose d'un volume suffisant de données chiffrées, qu'il a eu le temps de trouver la clé grâce à la puissance de ses outils de cryptanalyse. Il faudra donc donner à la clé une durée de vie inférieure au temps nécessaire estimé pour la découverte de la clé.
Plus la clé sera « compliquée », plus ce temps sera long, mais plus les temps de chiffrement et de déchiffrement seront longs eux aussi. Tout est donc ici affaire de compromis.
3-7. Le tiers de confiance▲
Vous l'avez compris, cette magnifique mécanique ne fonctionnera qu'à une condition : le « concierge » (CA(3)) qui détient les clés publiques doit être digne de confiance, faute de quoi, n'importe quoi peut se produire…
Que pourrait-il arriver si une clé publique n'appartenait pas réellement à la personne indiquée ? Tout simplement une personne pourrait se faire passer pour une autre. Une fausse carte d'identité, en quelque sorte.
Tout repose donc sur la confiance que l'on peut mettre dans la personne qui détient les clés publiques.
Généralement, il s'agit d'un organisme de réputation sérieuse, à qui l'on confiera sa clé publique, et dont on détient la clé publique de façon sûre. La clé publique de l'organisme permettra de vérifier l'authenticité dudit organisme.
3-8. Les certificats▲
Il existe dans le monde plusieurs organismes (CA) de ce type. Leurs services, est-il nécessaire de le dire, ne sont pas gratuits, loin de là .
Lorsque je m'adresse à un tel organisme pour récupérer une clé publique, il me l'enverra avec un certificat. En gros, il s'agit pour ledit organisme de chiffrer la clé publique demandée, ainsi que quelques informations supplémentaires sur le propriétaire de cette clé, avec sa propre clé privée, pour authentifier son envoi. Il me reste à disposer de la clé publique du tiers de confiance, par un moyen sûr. Les certificats sont à la norme X.509.
Si je suis sûr de la clé publique du tiers et si j'ai confiance en lui, alors je pourrai mettre aussi ma confiance dans les clés publiques qu'il me distribuera.
Votre navigateur a installé, peut-être à votre insu, des certificats de divers organismes de certification (exemple avec Mozilla Firefox) :
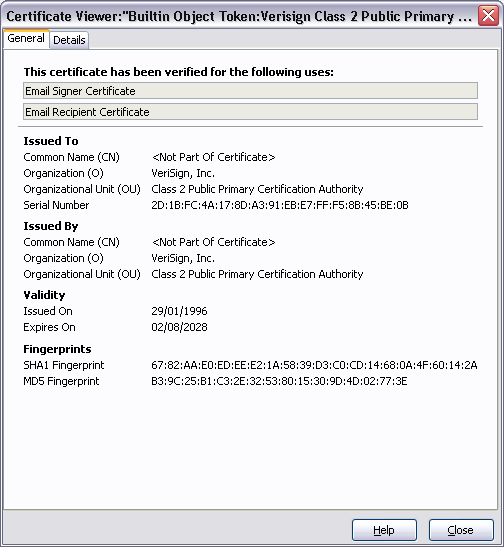
Voici un résumé du contenu d'un certificat :
Et bien entendu, le certificat contient une clé publique :
Comme une clé s'use (le volume de données chiffrées avec devient trop important, ce qui risque d'augmenter significativement les chances de découverte de cette clé), il faudra prévoir une durée de vie à cette clé et donc au certificat.
Comme une clé peut se perdre ou être volée, il faudra aussi prévoir un système « d'opposition ». Une liste de révocation, qui permet de signaler les certificats non encore expirés, mais qui ne sont plus dignes de confiance pour une raison quelconque. La CA se doit donc de tenir à jour une liste de révocation, et, lorsqu'un utilisateur doit user d'un certificat qui est déjà en sa possession, il devrait commencer par vérifier si celui-ci n'a pas été révoqué entre temps.
Comme nous sommes dans un monde imparfait (d'ailleurs, si nous étions dans un monde parfait, les clés ne seraient d'aucune utilité), il peut se faire que l'usage de certains types de clés particulièrement « solides » soit réglementé. Il peut se faire qu'un exemplaire de la clé privée doive être mis sous séquestre, à disposition éventuelle des services de renseignements. Des organismes spécialisés dans cette mise sous séquestre de clés privées existent à cet effet.
3-9. Arbres et rĂ©seaux de confiance▲
Normalement, si deux interlocuteurs disposent chacun d'un certificat, mais chez des CA différentes, ils ne peuvent a priori se faire mutuellement confiance, sauf si par un procédé quelconque les deux CA affichent une confiance mutuelle. Entrer ici dans les détails nous mènerait vraiment trop loin, mais sachons tout de même que :
- les autorités de certification sont hiérarchisées, il y a des autorités racines et des autorités intermédiaires, ce qui aboutit à une structure arborescente. Si deux autorités intermédiaires sont certifiées par une même autorité hiérarchiquement supérieure, elles appartiennent au même arbre et donc la confiance est mutuelle, nous avons ici un arbre de confiance ;
- deux arbres différents peuvent à un niveau quelconque (mais supérieur à celui des partenaires impliqués), établir entre eux un lien de confiance mutuelle, ce qui donne naissance à des réseaux de confiance.
3-10. Le rĂ©seau de connaissances▲
Une autre méthode consiste à utiliser un réseau de connaissances. J'ai, en principe, confiance dans mes amis et les amis de mes amis sont mes amis, donc, je peu faire confiance à une clé publique qui est contresignée par un ami dont je suis sûr. Ça peut aller loin, c'est le principe de l'homme qui a vu l'homme qui a vu l'homme qui a vu l'homme qui a vu Dieu.
C'est aussi le principe adopté en messagerie électronique par des procédés de signature comme GNUpg.
3-11. Les PKI▲
Les Public Key Infrastructures regroupent tout ce qui est nécessaire à la gestion des clés publiques et des certificats :
- récupération des demandes de certificats ;
- réalisation des certificats ;
- tenue de la liste de révocation,
- distribution des certificats aux demandeurs…
Lorsqu'une organisation désire mettre en place une telle infrastructure, sans avoir recours à des entreprises spécialisées, il lui est possible de le faire.
Bien entendu, les certificats produits n'auront de valeur qu'au sein de cette organisation. Il existe des projets Open Source qui proposent des outils de gestion d'infrastructure de clés publiques. Nous n'irons pas aussi loin dans cet exposé.
3-12. Bref…▲
Le principe est donc assez simple, il faut au départ disposer de clés publiques appartenant à des gens dont on est sûr. Si ces gens dont on est sûr me certifient comme étant authentiques des clés de gens que je ne connais pas, ces clés publiques seront à leur tour réputées sûres.
Vous voyez la limite d'un tel système ? Non ? Alors, imaginez que dans la chaîne, il y ait une clé falsifiée qui passe pour authentique, à la suite d'une malversation quelconque. Alors, toutes les clés certifiées par cette clé falsifiée pourront être ou ne pas être authentiques…
Il est donc assez illusoire d'imaginer ce système comme parfaitement sûr. Fort heureusement, dans la plupart des cas, un seul administrateur certifiera les clés dont nous aurons besoin pour, par exemple, créer un tunnel sécurisé ou simplement une authentification entre deux nœuds d'un même réseau.
3-13. Ă€ quel niveau chiffrer▲
Dans la pile des protocoles réseau, il est courant d'utiliser le chiffrement :
- dans le noyau du système, au niveau IP, avec IPsec. Ainsi, tout ce qui passera sur le réseau sera automatiquement chiffré suivant les règles établies sans que les applications n'aient à s'en soucier ;
- dans l'espace utilisateur, au niveau des applications elles-mêmes, qui choisiront ou non de chiffrer, avec par exemple, SSL. HTTPS en est une illustration, comme IMAPS, POPS ou encore SSH.
SSL, développé au départ par Netscape a été repris en open source sous le nom de TLS : Transport Layer Security. Protocole de sécurisation de la couche transport, défini par la RFC 2246. La version 1.0 de TLS est en fait SSL v3.
4. Mise en Ĺ“uvre avec TinyCA▲
Nous aurons l'occasion de mettre en pratique diverses méthodes de chiffrement dans le tunnel OpenVPN et aussi dans la sécurisation d'un réseau WI-FI, sans oublier également SMTP, POP3 et IMAP sécurisés.
Nous allons plutôt ici nous intéresser à la réalisation d'une mini « CA » à l'aide d'OpenSSL. Présent sur toutes les distributions GNU/Linux, cet outil se présente sous forme de commandes en ligne dont l'ergonomie n'a d'égale que la complexité de l'outil.
Plus avenant, TinyCA propose une interface graphique pour manipuler les diverses commandes d'OpenSSL de façon plus compréhensive. Nous allons donc réaliser au moyen de TinyCA :
- une autorité de certification « maison », avec son propre certificat ;
- un certificat pour un serveur, contresigné par notre autorité « maison » ;
- un certificat pour un client, également contresigné par notre autorité « maison ».
Notons que TinyCA n'est pas une PKI(4). Il ne fait rien de plus que ce que sait faire OpenSSL.
4-1. Rappels▲
Rappelons tout de même brièvement ce qu'est un certificat.
L'objectif est de pouvoir distribuer une clé de chiffrement publique, avec tout ce qu'il faut comme informations pour :
- identifier clairement le propriétaire de cette clé publique ;
- obtenir « l'assurance » de l'authenticité de ce certificat.
Le second point est obtenu par la signature dudit certificat par une autorité « de confiance », elle-même pouvant être certifiée par une autorité supérieure, etc. Dans un tel cas, le certificat doit contenir les informations nécessaires pour pouvoir remonter et obtenir si besoin est les certificats des autorités successives, jusqu'à l'autorité « ultime ».
Dans le vaste monde numérique, il existe une certaine quantité « d'autorités ultimes » reconnues comme telles, le plus souvent commerciales, qui peuvent délivrer des certificats à qui en fait la demande, moyennant finances.
Parallèlement, une entreprise peut très bien créer sa propre autorité « racine » et authentifier des certificats qu'elle émet pour les besoins de son entreprise (ou même de ses clients). Nous allons opérer dans ce cadre.
4-2. Utilisation de TinyCA▲
TinyCA (plus exactement TinyCA2) est développé en perl-GTK2. Il est disponible dans sa dernière version pour Debian, Ubuntu…
Nous allons créer une CA, un certificat pour un serveur, un autre pour un client. Enfin, nous exporterons le nécessaire sous une forme que GNU/Linux aime : le format « pem ».
4-2-1. CrĂ©ation de la CA▲
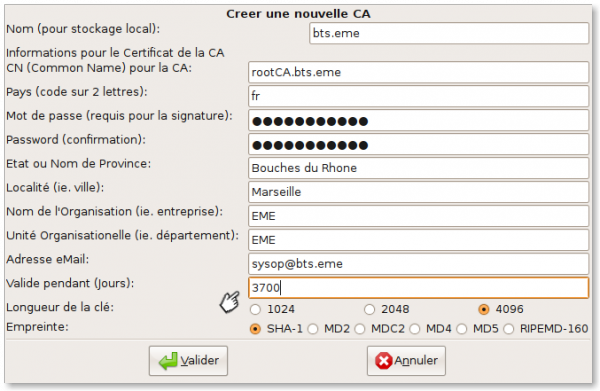
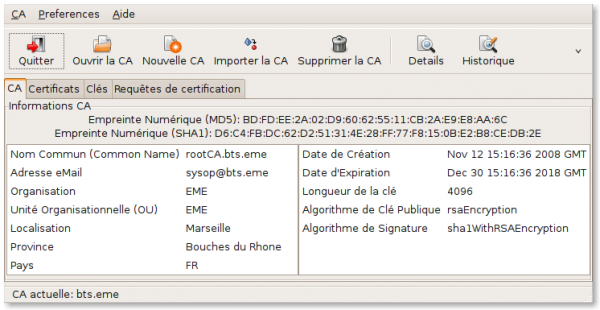
Nous ouvrons TinyCA2 et demandons la création de la CA :
Ceci nous amène à remplir un premier formulaire :
Dans l'exemple, notre organisation s'appelle « EME » et notre domaine sera bts.eme.
Le mot de passe saisi sera demandé à chaque validation de demande de certificat par la CA. Il faut bien sûr :
- le choisir solide ;
- ne pas l'oublier.
Prenez garde à la durée de validité. Une validité courte obligera à renouveler rapidement les certificats. La date de fin de validité de la CA impose une date de fin de validité inférieure ou égale à tous les certificats qu'elle approuvera.
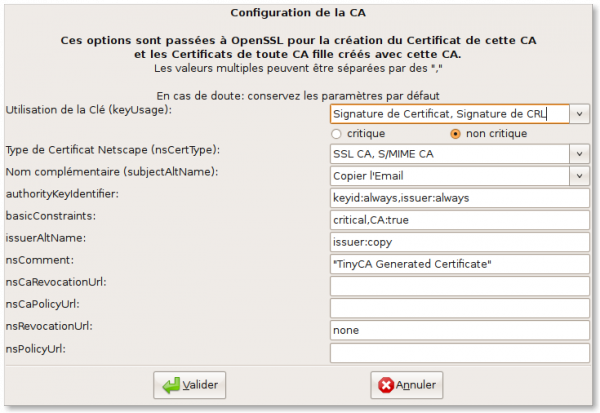
Après avoir rempli et validé ce formulaire, il en vient un autre :
Les options par défaut conviendront dans la plupart des cas. En cas de doute, consultez la documentation d'OpenSSL (rappelons-nous que je ne suis pas un spécialiste des PKI). Au bout du compte, nous disposons maintenant de notre CA, avec son certificat. Rappelons que celui-ci servira à authentifier les divers certificats que nous allons créer par la suite.
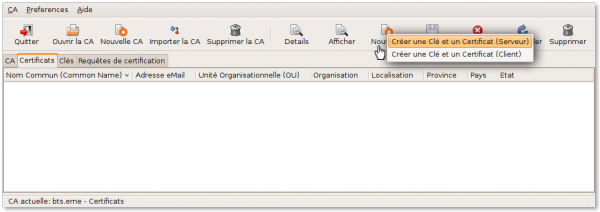
4-2-2. Certificat du serveur▲
Nous allons maintenant créer le certificat du serveur, ainsi que sa clé privée. « Nouveau certificat » :
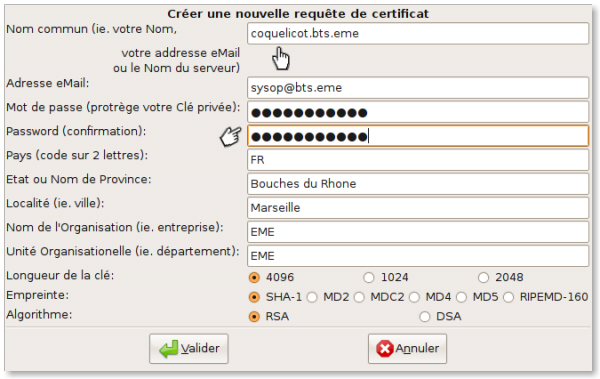
Ceci va avoir pour effet de générer une requête de certificat :
Le serveur s'appelle coquelicot et se situe dans le domaine bts.eme. Le mot de passe demandé ici est destiné à protéger la clé privée qui va être générée, en cas de vol de cette dernière. Même si nous désirons en définitive utiliser une clé non protégée par mot de passe, ce qui est parfois nécessaire lorsque cette clé est manipulée par des logiciels (OpenVPN par exemple), nous devons ici saisir un mot de passe.
Le reste des informations est fourni par défaut. Il peut être préférable de choisir l'algorithme DSA, réputé plus solide, pour l'usage de la clé privée.
Nous allons maintenant faire signer cette requête par la CA, créant ainsi le certificat et la clé privée pour le serveur :
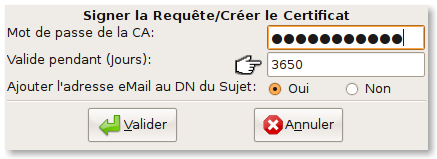
Prenez soin d'indiquer une durée de validité qui ne dépassera pas celle de la CA au moment où vous signez le certificat. De toute manière, TinyCA vous alertera s'il y a dépassement de durée.
Le mot de passe demandé ici est bien entendu celui que vous avez fourni lors de la création de la CA (celui que l'on a fait solide et que l'on n'a pas oublié).
Le certificat du serveur est créé, ainsi que sa clé privée. Nous finaliserons lors de l'exportation de tout ceci.
4-2-3. Certificat du client▲
La procédure est rigoureusement identique, hormis que l'on aura choisi de créer un certificat pour un client. Nous ne la détaillerons donc pas ici. Le client s'appelle Betelgeuse est se trouve dans le domaine maison.mrs.
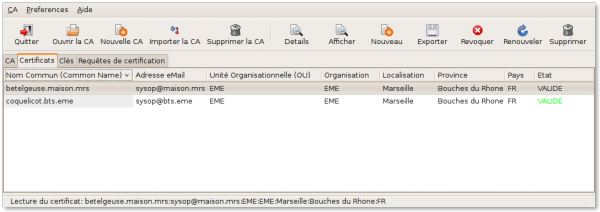
Nous pouvons vérifier que les certificats et les clés privées sont bien créés et valides dans TinyCA aux onglets respectifs :
Il ne nous reste plus qu'Ă exporter tout ceci au format pem.
4-2-4. Export des clĂ©s et certificats▲
Une fois les certificats créés, nous devons les empaqueter dans des conteneurs normalisés. Il existe plusieurs formats de conteneurs, les plus couramment utilisés étant sans doute pem, der et pkcs#12.
pem comme pkcs#12 sont des conteneurs qui peuvent inclure non seulement le certificat x509 (avec la clé publique), mais également la clé privée associée, le tout protégé par un mot de passe, pour protéger la clé privée.
Nous allons utiliser ici le conteneur pem (Privacy Enhanced Mail), mais nous empaquetterons le certificat et la clé privée dans des conteneurs différents.
4-2-4-1. La CA d'abord▲
L'ordre n'a bien entendu pas d'importance, mais commençons par le plus simple, puisqu'ici il n'y aura pas de clé privée à exporter. Rappelons que la clé privée est « privée » et que celle de la CA ne doit pas quitter la CA. Il n'y a donc pas à l'exporter :
Choisissez un chemin judicieux pour l'exportation ainsi que le format d'export (pem en ce qui nous concerne).
4-2-4-2. Pour coquelicot▲
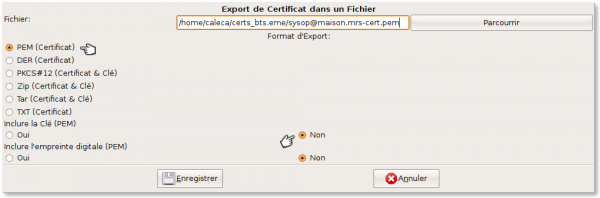
Commençons par le certificat. Nous travaillons toujours au format pem :
Ce format permet d'intégrer la clé privée dans le certificat. Nous ne le ferons pas, préférant placer la clé dans un fichier séparé.
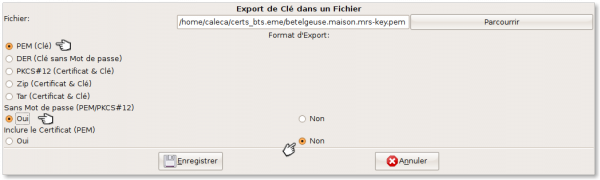
Passons à l'export de la clé privée :
Nous l'exportons sans mot de passe, à cause de l'usage qui lui est destiné (OpenVPN en l'occurrence), sans y mettre le certificat, dont nous disposons déjà .
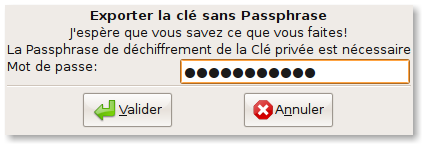
Bon gros avertissement sur les risques de cette opération. TinyCA couine, mais s'exécute quand même. Le mot de passe demandé est bien évidemment celui qui a été fourni lors de la création du certificat.
4-2-4-3. Pour Betelgeuse▲
La procédure étant exactement la même, nous ne détaillerons pas non plus. Finalement, nous retrouvons dans notre répertoire d'export, les fichiers suivants :
- bts.eme-cacert.pem, le certificat de la CAÂ ;
- betelgeuse.maison.mrs-key.pem, la clé privée de Betelgeuse ;
- betelgeuse.maison.mrs.pem, le certificat de Betelgeuse ;
- coquelicot.bts.eme-key.pem, la clé privée de coquelicot ;
- coquelicot.bts.eme.pem, le certificat de coquelicot.
Évitons de nous faire piquer les clés privées, qui ne sont pas protégées…
5. Remerciements Developpez▲
Vous pouvez retrouver l'article original ici : L'Internet Rapide et Permanent. Christian Caleca a aimablement autorisé l'équipe « Réseaux » de Developpez.com à reprendre son article. Retrouvez tous les articles de Christian Caleca sur cette page.
Nos remerciements Ă ClaudeLeloup pour sa relecture orthographique.
N'hésitez pas à commenter cet article ! Commentez ![]()